Seine harmonischen Spekulationen führen Kepler zu wichtigen Erkenntnissen. Zuerst gelingt ihm der geometrische Nachweis zweier bisher unbekannter Sternpolyeder. Seine wichtigste Entdeckung aber ist das
Dritte Keplersche Gesetz:
Die Quadrate der Umlaufszeiten zweier Planeten verhalten sich wie die dritten Potenzen ihrer mittleren Abstände.
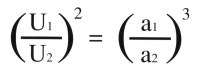
Bereits in seinem Erstlingswerk sucht Kepler nach einem Verhältnis zwischen den Umlaufszeiten und den mittleren Abständen der Planeten von der Sonne. Die in seiner "Harmonice Mundi" gefundene Beziehung hat einen großen Vorteil: Vergleicht man die Potenzen, verhält sich der Quotient der Umlaufszeiten zum Quotienten der mittleren Abstände wie 2:3. Es handelt sich also nicht um irgendeine Proportion, sondern um das Teilungsverhältnis der Quinte. Da das Gesetz vollkommen mit den Beobachtungsdaten übereinstimmt, scheint es Keplers harmonische Spekulationen mit den Vielecken zu bestätigen.
