Astronomia Nova "Der Kampf mit Mars"
Nachdem Sie durch die Benutzung der Treppe den Aufstieg Keplers zum Kaiserlichen Mathematiker quasi mitgemacht haben, können Sie sich im größten Raum des Museums ausführlich mit Keplers astronomischen Lebenswerk auseinandersetzen. Der Bereich gliedert sich in drei Ausstellungsgruppen:
- Die Erneuerung der Astronomie (Das Lebenswerk von Tycho Brahe und die "Astronomia Nova" von Johannes Kepler)
- Tabulae Rudolphinae
- Keplers Studien zur Optik
Die komplizierten astronomischen Zusammenhänge lernen Sie mit Hilfe der modernen Technik: Computerprogramme klären Sie über das Zustandekommen der Schleifenbewegungen von Mars, Jupiter und Saturn auf, führen Sie in die Welt der Keplerschen Gesetze ein und simulieren die Sonnenfinsternis vom August 1999. Die Palette der aufrufbaren Simulations-Programme wird laufend erweitert.
Kepler soll als Kaiserlicher Mathematiker astronomische Tafeln erstellen, die grundlegende Berechnungen zum Lauf der Himmelskörper enthalten. Da alle bisherigen Tafelwerke große Ungenauigkeiten aufweisen, versucht er, am Beispiel der komplizierten Marsbahn eine verbesserte Bahntheorie zu erarbeiten. 1609 veröffentlicht Kepler nach acht Jahren mühsamen Forschens die "Astronomia Nova". Sie enthält die entscheidenden Argumente für das Heliozentrische Weltbil und bricht mit dem fast zweitausend Jahre altem Dogma einer gleichförmigen Kreisbewegung der Planeten. Keplers erste Bahnhypothese beruht noch auf dem Prinzip der Kreisförmigkeit. Sie liefert gegenüber Brahes Beobachtungen Abweichungen von 8 Winkelminuten. Das Vertrauen in dessen mit nur einer halben Winkelminute Ungenauigkeit behafteten Messungen, läßt Kepler nicht ruhen. Er bricht mit der Kreishypothese und findet nach Irrwegen das:
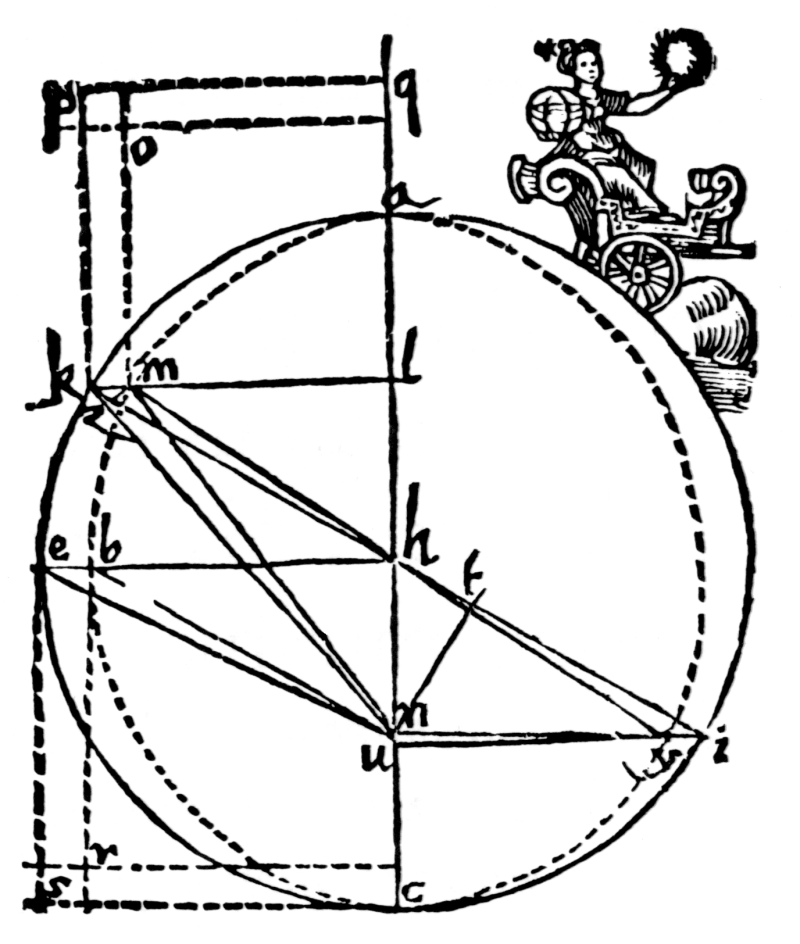Erstes Keplersches Gesetz Aus: Johannes Kepler: "Astronomia Nova", Prag 1609. 59. Kapitel
Erste Keplersche Gesetz
Die Planeten bewegen sich in Ellipsen, in deren einem Brennpunkt die Sonne steht.
Die Figur auf dem Wagen ist Urania, die Göttin der Astronomie. Sie hält für den Entdecker der elliptischen Bahnform den Lorbeerkranz des Siegers bereit. An dieser Figur lässt sich weniger die Eitelkeit, sondern vielmehr die Erleichterung Keplers ablesen, die er empfindet, als er nach vielen Irrwegen den Kampf mit Mars endlich siegreich beendet kann. Die elliptische Planetenbahn ist gestrichelt dargestellt. Sie weicht nur sehr geringfügig vom Kreis ab. Kepler geht davon aus, dass der Sonne magnetische Antriebskräfte innewohnen, die ungleichförmige Geschwindigkeiten der Planeten auf ihren Umlaufbahnen bewirken. Diese Idee einer "Physik des Himmels" führt ihn zum:
Zweiten Keplerschen Gesetz:
Der Fahrstrahl Sonne-Planet überstreicht in gleichen Zeiten gleiche Flächen.
Der Flächensatz ist deswegen so bedeutend, weil er mit dem uralten Dogma einer gleichförmigen Bewegung der Planeten um die Sonne bricht. Da der Fahrstrahl in gleichen Zeiten gleiche Flächen überstreicht, muß er sich der Planet in Sonnennähe schneller und in Sonnenferne langsamer bewegen. Dies paßt zu genau zu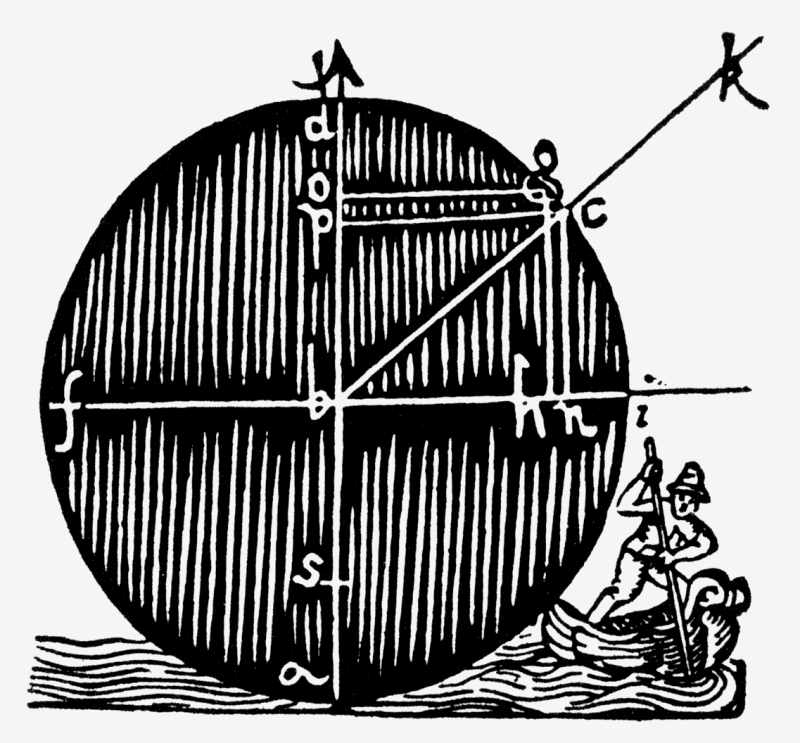 
Allegorische Darstellung der Radialkraft Aus: Johannes Kepler "Astronomia Nova", Prag 1609. Letzte SeiteKeplers Vorstellung von der Wirkung zweier Magnetkräfte. Heute wissen wir. dass die ungleichförmige Bewegung der Planeten und die Stauchung des Kreises zur Ellipse von der mit dem Quadrat der Entfernung abnehmenden Gravitationskraft der Sonne herrührt.
Der schwarze Kreis stellt den Planeten dar, die weißen Linien symbolisieren die magnetischen Kraftlinien. Die von b über c nach k verlaufende Strecke deutet in Richtung Sonne. Der Fährmann ist für Kepler das geeignete Symbol für die Radialkraft des Planeten: Man stelle sich eine Fähre vor, die an einem quer über den Fluss reichenden Seil befestigt ist. So wie die Strömumg für den Antrieb sorgt und das Ruder die Fahrtrichtung vorgibt, sorgt die Zirkularkraft für den Antrieb, die Radialkraft für die
Abstandsänderung des Planeten zur Sonne. Die Radialkraft ist also eine wechselwirkende Kraft.